ABSTRACT.

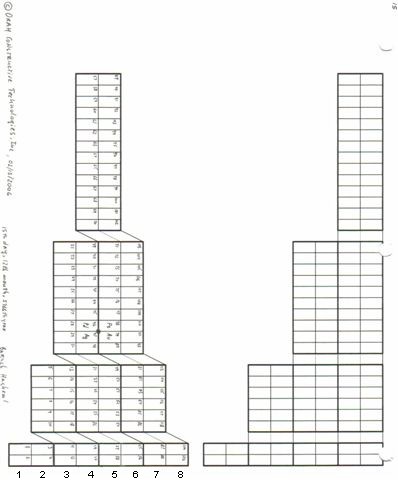
ADOMAH Periodic Table is based on the Left Step Periodic table that was introduced by Janet in 1928. It consists of four blocks (f, d, p and s) that correspond to the quantum numbers l = 3, 2, 1, 0. Blocks are separated from each other, shifted and reconnected via diagonal lines. ADOMAH Table allows direct reading of the quantum number 'n' and can be presented in horizontal or vertical formats. In vertical format ADOMAH Table has vertical columns that correspond to the quantum number n = 1, 2, ..., 8 and cascades n + l = 1, 2, ..., 8 (if diagonal lines are followed when moving form block to block). The cascades provide continuity with respect to atomic number Z. Numbers at the bottom of the table represent either quantum number 'n', if columns are followed vertically, or 'n + l' if cascades are followed. This feature is very useful for writing electron configurations (see User Guide).

Quantum numbers ml and ms are addressed by placing elements in rectangular "boxes" with 1 x 1/2 proportions so that any two such "boxes" make up a square unit.

or Unit square used to establish proportions of spdf blocks and to bring them in compliance with number of values of quantum number ml corresponding to each block.

These seemingly cosmetic changes resulted in interesting observation: quantum numbers n, l, ml and ms and their interrelation can be explained on a basis of a three dimensional geometric shape that is known as Regular Tetrahedron (see 3D Image).

The Whole Story

1. Introduction.

The quantum mechanics in its present state can not fully explain all intricacies of the Periodic System in part because the quantum numbers n, l, ml and ms , that describe electronic populations of the atoms, are not completely understood in terms of mathematics.

Attention of scientists has almost always concentrated on the contents of the Periodic Table, but its geometric form has generally been viewed as an outcome of arrangement of the elements, or as a matter of preference. This article represents a serious attempt to analyze PT geometry based strictly on quantum numbers which define electron configuration of atoms (n, l, ml and ms) . It will be demonstrated here that analyzing PT geometry can lead us to a better understanding of quantum numbers and can help us to visualize their relationship to each other.

The quantum numbers that define electronic shells and their relation to each other can be explained on a basis of commonly known three dimensional shape. This geometric shape can be used as a visualization tool for further exploration of not only electron shells, but also atomic nuclei.

In order for us to begin serious discussion of PT geometry, IUPAC Standard PT has to undergo three simple logical transformations that will bring it closer to the agreement with the quantum numbers.

Step 1. Transformation of the Standard PT to the Left Step Periodic Table.

a) First we have to identify and mark all distinctive parts of the Standard PT as s, p, d and f ;

b) assign angular momentum quantum numbers l = 0, 1, 2 and 3 to the corresponding sub shells s, p, d and f and move element He to its appropriate place in the s-block. (Just as gas nitrogen and non-metal phosphorus are located in the same group with metal bismuth, inert helium, because of its atomic structure, should be placed in the same group with alkaline earth metals).

e) and finally, move s-block to the right of p-block and move the footnote f-block to the left side of the table, so that the quantum numbers l are in correct order (3,2,1,0).

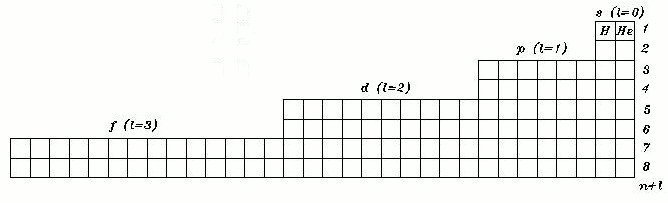
This PT formulation is known as the Left Step Periodic Table (LSPT), first published by Charles Janet in 1928.

Step 2. Correlating the primary quantum numbers with the rows.

Despite its orderly look, the LSPT has three draw backs: it does not allow direct reading of the quantum numbers 'n' (its rows represent n + l ); it does not have symmetry and it has disproportional length comparatively to its height.

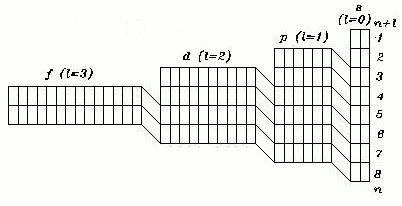
First two deficiencies can be easily fixed by, separating the blocks from one another and by moving up each block by a number of units equal to the quantum number l, corresponding to each particular block.

Now the number of each row corresponds to the primary quantum number 'n' and each layer, or strata, corresponds to the sum of the quantum numbers n + l.

Coincidently, this operation has also addressed the question of the symmetry .

Step 3. Defining the correct proportions.

As it was noted above, PT proportions need to be addressed. At first it seems that this is just a matter of preference, or pure cosmetics, but, unlike its dimensions, proportions of the PT can be determined objectively. Lets define the meaning of each quantum number in terms of the PT geometry:

It should be noted that first three quantum numbers are integers, but the last one, the spin quantum number, is a fraction. The fact that electron spin can be described by a single quantum number whose value can be only s=1/2 was confirmed by Paul Dirac in 1929. Given that each entry in the PT represents a single element, determined by one electron/proton pair, conclusion can be made that one dimension of each cell has to be associated with the absolute value of the spin quantum number ms, that is 1/2. The other dimension shall be associated with the minimum value of the quantum number 'n' and shall be equal to unity.

Therefore, proportions of each cell of the geometrically correct Periodic Table have to be 1/2 : 1, not 1: 1 or so, as currently used by the Standard PT. That is, one unit square comprising two rectangular cells is used as a measure to proportion spdf blocks in order to reflect number of ml values corresponding to each block. or

Now, we can cut the length of each cell, each block and the total length of the PT in half and do it on the totally objective basis. (So much for cosmetics).

This PT formulation was discovered by the author of this article on February 13, 2006 and is known as The ADOMAH Periodic Table.